Challenge

Background

The development of a Planetary defence capability is only at its early stages for humankind. Following the pioneering work of scientists such as Andrea Milani [1], ESA has been considering the use of space missions to prepare for an asteroid deflection effort since two decades [2-5]. Several techniques have been proposed to avoid an Earth impact event by altering the trajectory of an asteroid on a collision course with Earth. Among these proposals, the one that is currently being considered as more mature, because it is based on existing and affordable spacecraft technology, is the kinetic impactor, which changes the orbit of an asteroid by a direct hit of a spacecraft at a very high relative speed (several km/s).

The actual effects of such an impact are very uncertain due to the so called $\beta$ factor [5], measuring the actual exchange of linear momentum between the impactor and the target body.

The Challenge

Several high-fidelity simulations of a kinetic impactor mission over a binary system have been produced (and kept hidden from you). The lightcurves as observed from the Earth before and after the impact of each of the simulated scenarios are available. For some of them (the training set) critical parameters such as $\beta$, the primary $J_2$ and the ratio between the secondary major and minor axis are also released. For the remaining ones (the test set), it is your task to produce an estimate for them. Can you learn from the data only? Can the impact geometry and problem physics help you? We will find out :)

The binary system

Preliminary analysis has lead to identify the following facts on the binary system : the system consists of two objects of masses $M_P = 3 \cdot 10^{11} kg$ (called the "primary" $P$), and $M_S = 1.3 \cdot 10^9 kg$ (called the "secondary" $S$) in a relative circular orbit with an unknown separation between the centers of masses. The secondary is tidally locked with the primary.

The primary body is an oblate spheroid with an uncertain, but bounded, value of $J_2 < 0.15$ and an equatorial radius $R_P = 370m$. The secondary, has a nearly prolate shape, with the long axis $a$ laying on the plane of the relative orbit of the two bodies, and two equal minor axes $b = c$. The values and ratio of long to short axis is unkown.

Available light curves are consistent with values of the axial ratio in the range $1.3 < a/c < 2.5$. The secondary's long axis points towards the center of mass of the primary, while both bodies' spin axes are normal to the plane of the relative orbit (coinciding with the ecliptic and thus providing nice observation opportunity for light curves).

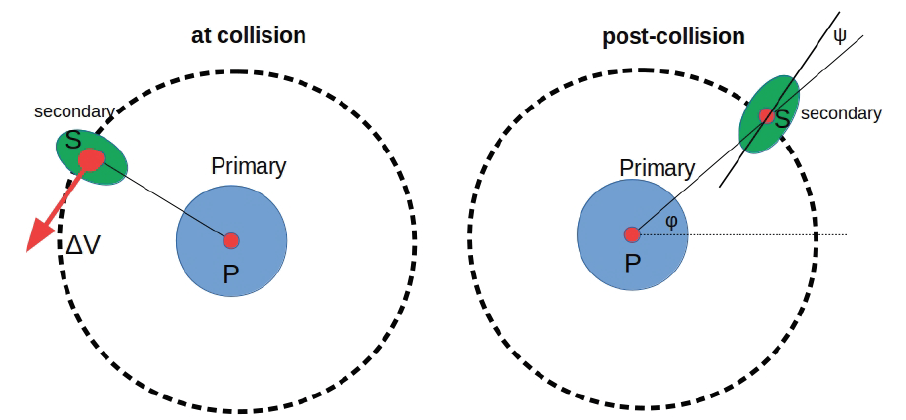
Relative orbit of the secondary around the primary before and after collision. S moves in the counter-clockwise sense. At the moment of the collision with the probe, the relative velocity of the probe with respect to the secondary is $\vec{\Delta V}$, tangent to the orbit in the direction indicated by the red arrow.

The kinetic impact

The beta factor of the probe-asteroid collision, is defined as: $$ \beta = P_1/P_0 $$ where $P_1$ is the linear momentum actually transfered to the secondary after the collision, and $P_0$ is the momentum that would have been transferred in case of a perfectly plastic collision. Due to the ejecta escaping from the system after the collision, we have $\beta \geq 1$.

The probe hits the secondary with a relative velocity vector $\vec{\Delta V}$ belonging to the plane of the $PS$ relative orbit, and being normal to the smallest meridian of the secondary. The mass of the impact probe is 700kg with an impact velocity of $\Delta V = 5 km/s$.

References

[1] Milani, Andrea, Steven R. Chesley, and Giovanni B. Valsecchi. "Asteroid close encounters with Earth: risk assessment." Planetary and Space Science 48.10 (2000): 945-954.

[2] Carnelli, Ian, Andrés Galvéz, and Franco Ongaro. "Learning to deflect Near Earth Objects: industrial design of the Don Quijote mission." 57th International Astronautical Congress. 2006.

[3] Izzo, Dario, et al. "Optimal trajectories for the impulsive deflection of near earth objects." Acta Astronautica 59.1-5 (2006): 294-300.

[4] Izzo, Dario. "Optimization of interplanetary trajectories for impulsive and continuous asteroid deflection." Journal of guidance, control, and dynamics 30.2 (2007): 401-408.

[5] Michel, Patrick, et al. "European component of the AIDA mission to a binary asteroid: Characterization and interpretation of the impact of the DART mission." Advances in Space Research 62.8 (2018): 2261-2272.

[6] Syal, Megan Bruck, J. Michael Owen, and Paul L. Miller. "Deflection by kinetic impact: Sensitivity to asteroid properties." Icarus 269 (2016): 50-61.